Природа в огромном количестве показывает нам красивые изгибы. Их можно увидеть в лепестках цветов, в листьях, в волнах, облаках, в потягивающихся кошках, в человеческом теле…

А вот когда пытаешься воплотить увиденное в собственном творчестве, то нередко испытываешь трудности.

Есть очень древний способ добиться изготовления красивых вещей с плавными изгибами: нужно сделать 1000 и более вещей с такими кривыми, чтобы глаза и руки прочувствовали как нужно делать.

Но мысль о том чтобы делать тысячу вещей, для понимания кривых приводит в уныние. Так что это не вариант.

И вот тут может помочь геометрия.

Небольшой секрет: чтобы сделать кривую нужно начинать с прямой линии.

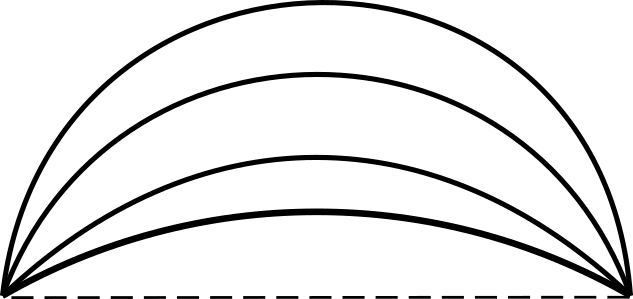
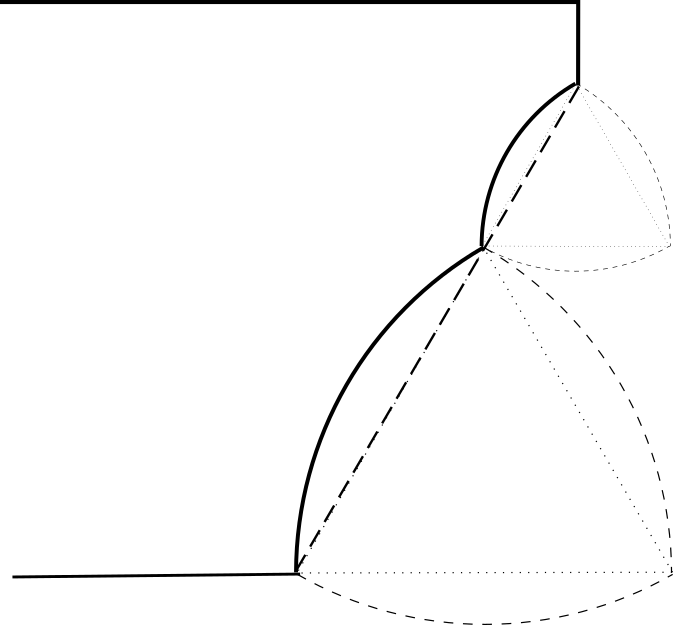
Здесь в качестве радиуса можно использовать либо весь отрезок между точками дуги, либо его половину, и в зависимости от выбора центра получить разные дуги.

Чтобы лучше это понять предлагаю посмотреть на несколько примеров.

В них будет использоваться одна дуга с радиусом равным отрезку прямой между концами дуги (хорда) и центром равноудаленным от концов отрезка. То есть кривая опирается на равносторонний треугольник (угол 60°).

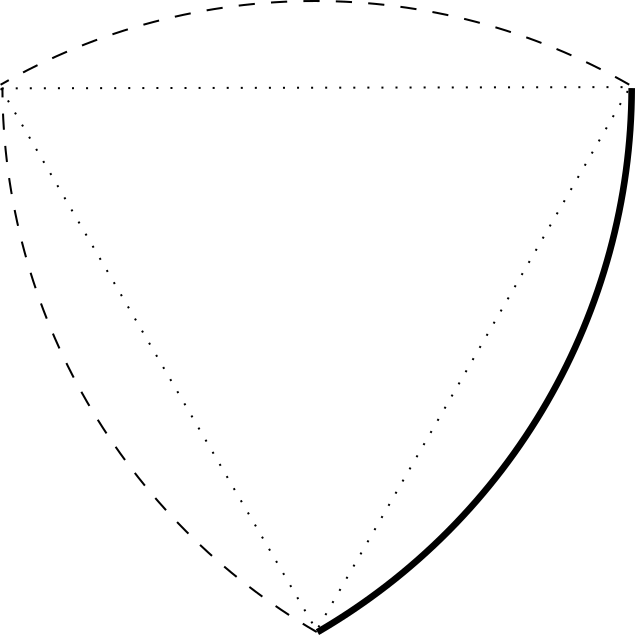
Даже такая простая кривая, равная 1\6 окружности позволяет делать красивые изгибы.

Сильно напоминает профили различных фрез.

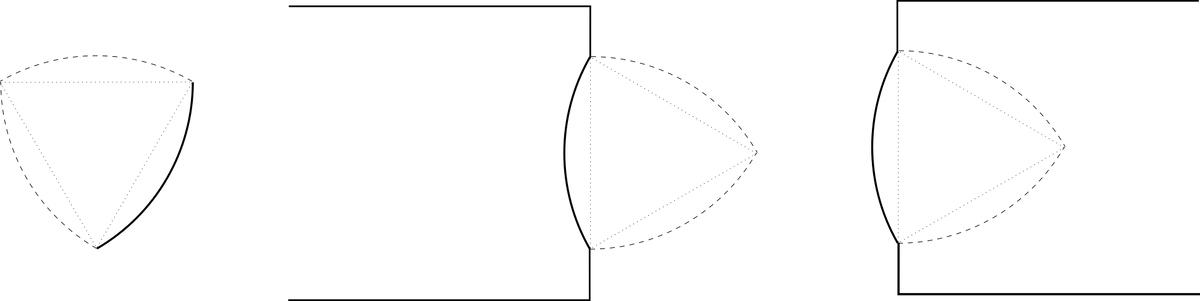
Или на основе только этой дуги можно выточить чашу, кубок или бокал.

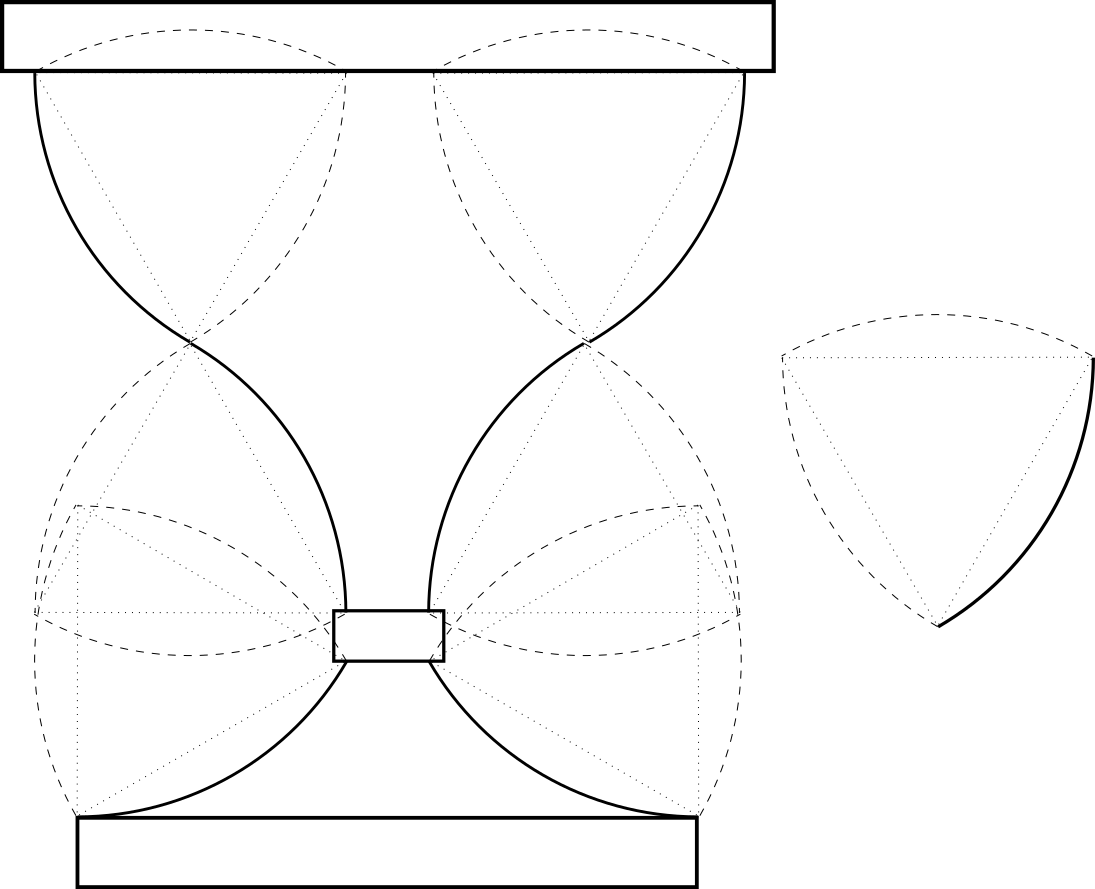
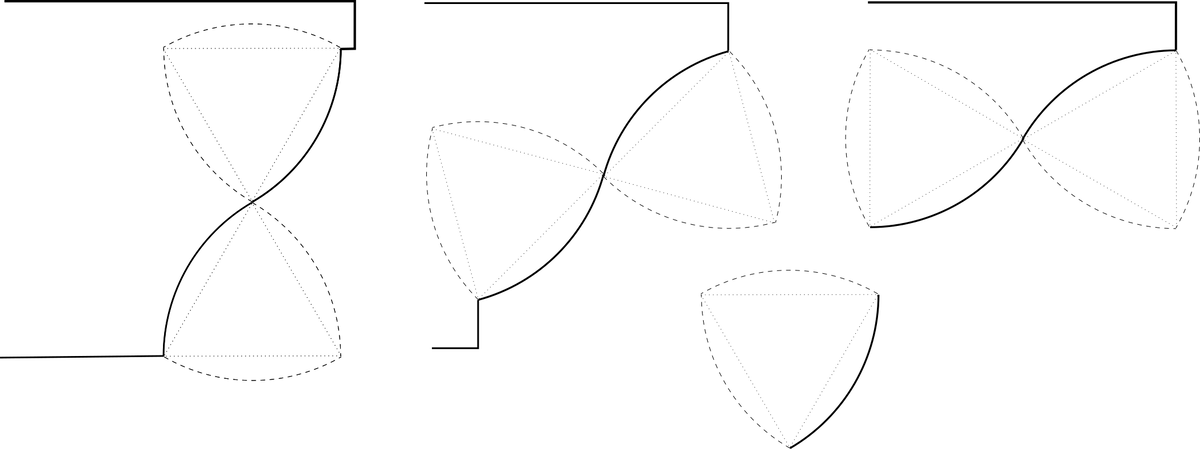
1\6 часть окружности, дуга на одном отрезке, и даже только это даёт много возможностей для создания красивых изделий из дерева. Разные углы расположения, разный ритм, дуги соединённые разными отрезками прямой.

Это, как всего лишь одна нота в музыке, а что возможно сделать, если таких нот будет больше

А как использовать разные радиусы, чтобы гармония сохранялась?

Здесь есть ещё один секрет: концы дуг с разными радиусами должны лежать на одной прямой.

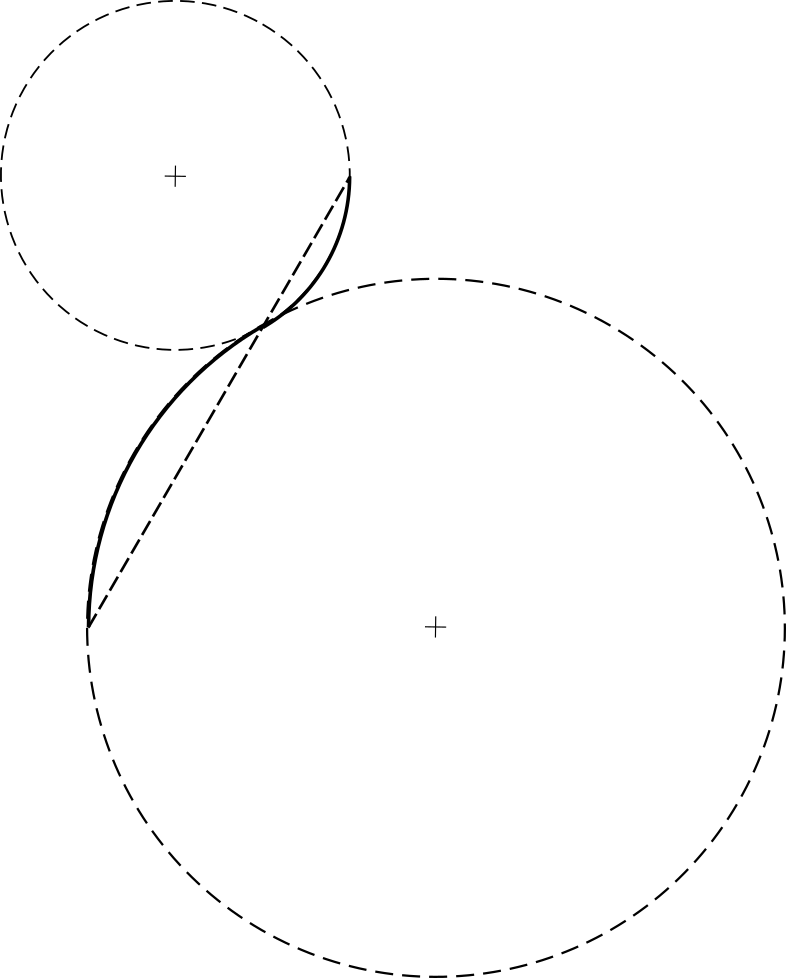
И вот тут начинается игра ритмов. Отрезок ведущей прямой можно разделить пропорционально на несколько частей 1:1, 2:3, 3:5 и так далее.

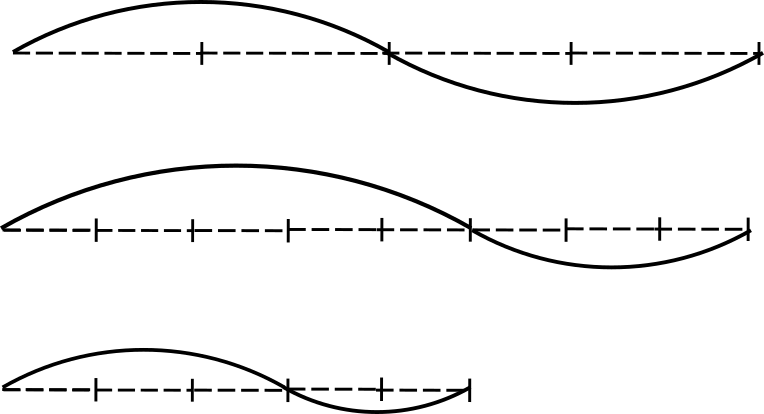
Кривые могут быть и более сложными и чередовать вогнутость и выпуклость в разных пропорциях.

При этом концы всех изгибов располагаются на одной прямой.

На основе этого можно уже строить разнообразные сложные профили и фигуры.

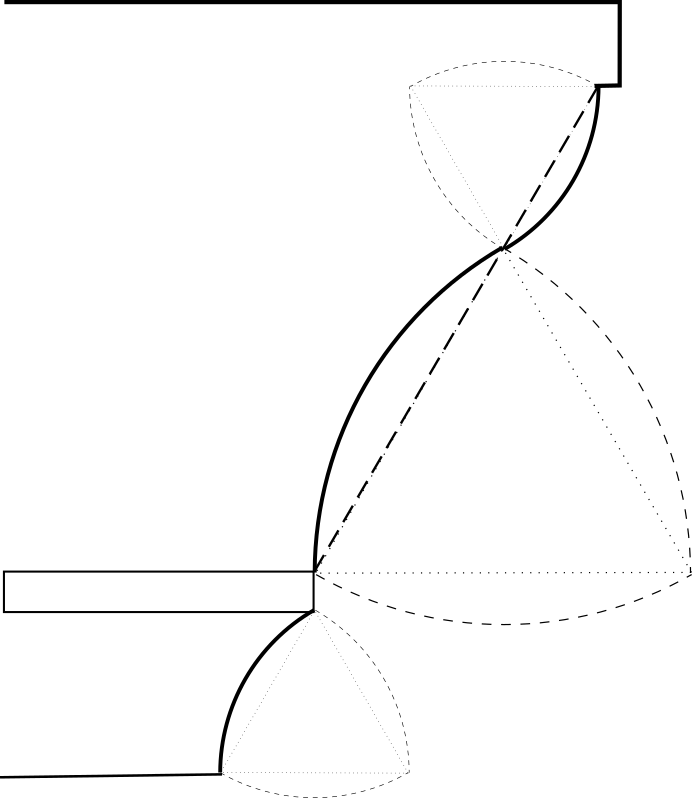
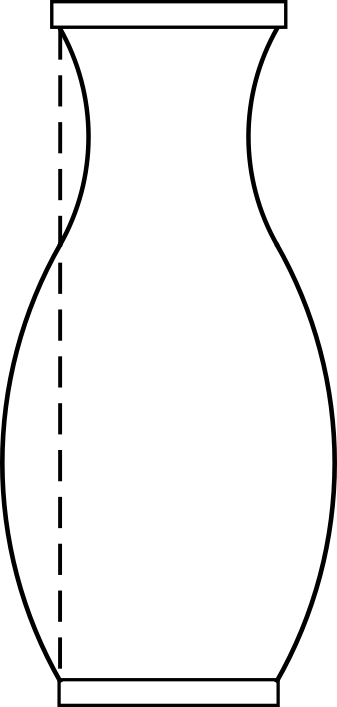
Получается что можно построить форму из прямых, а затем на основе этих прямых выстроить плавные кривые.

В качестве примера посмотрите на фото разных балясин, которые я нашел на просторах интернета.

В примерах выше через конечные точки кривых всегда можно провести прямые, даже когда эти кривые разделены прямыми участками.

Успехов в создании плавных кривых.

Спасибо что дочитали.

Чтобы быть в курсе новинок, подписывайтесь на мой телеграмм «Столярка дома с Александром Климовым»